最近看到一个新闻，武汉开展全城新冠病毒核酸检测，要在 10 天内检测全市 1000 多万人中病毒携带者，这无疑是一个巨大的工程。这里我不打算深究医护人员是采用什么方式完成这项任务，主要想从这个检测事例中，引出一个有意思、又很有实践意义的问题：有 N 瓶无色无味液体（N 可能很大，如 100，1000，10000 等），其中混入了一瓶有毒液体，同时也有试剂，可以检测液体的毒性，如果试剂滴入到有毒液体中，液体变蓝，否则不变色，除此之外，不能通过其他方式检测。问题来了，如何用最少的检测次数，找到这瓶有毒液体。

这是一类问题，网上也能找到很多类似变种，如用小白鼠检测毒药，但本质都是一样的。回到上述这个问题，最直观的办法，当然是一瓶一瓶的检测，最坏的情况下，需要 N -1 次才能找到有毒的那瓶，有没其他更快的办法呢？学计算机的都知道二分查找，又叫折半查找，但这个问题条件不具备有序性，是没法用二分查找的。

我们不妨把问题简化下，假如 N=2，即在 2 瓶液体中找到有毒的那瓶，这就简单了，随便把试剂滴入一瓶液体中，如果这瓶液体变蓝，则找到，有毒的就是这瓶，如果没变蓝，那有毒的就是另一瓶。所以，N=2 时，检测一次，可以确认有毒液体。 把 N 加大点，当 N=4 时，如何快速找到有毒的那瓶呢？可以这样，把 4 瓶液体均分为 A，B 两组，将每组的两瓶液体取少量混合放入新瓶，这样会得到两瓶混合液体，用试剂检测这两瓶混合液体，问题又变成上面 N=2 的情况了，假如 A 组的混合液体变蓝，说明有毒液体是 A 组两瓶液体中的一瓶，再检测一次，可以确定有毒液体；假如 A 组的混合液体没变蓝，那有毒液体是 B 组两瓶液体中的一瓶，再检测一次，同样可以确定有毒液体。用这种方式，N=4时，检测两次，就可以确认有毒液体。 当 N=8 时，我们同样先分为 A，B 两组，将每组的 4 瓶液体取少量混合，用试剂检测两瓶混合液体，假如 A 组的混合液体变蓝，说明有毒液体是 A 组 4 瓶液体中的一瓶，问题回到 N=4 的情况了，再测两次，即可确认有毒液体。 所以，当 N=8 时，共检测 3 次，可以确认有毒液体。 那么，当 N=16 时，共需要检测 4 次，可以确认有毒液体。这比一瓶一瓶的检测快多了。那么，假如 N 不等于 2、4、8、16 这种 2 的 n 次幂时，怎么办呢？其实是一样的，例如 N=7，还是可以先分两组，一组 4 瓶，一组 3 瓶，后面的流程类似。于是，我们可以得到一个一般性结论：当有 $N$ 瓶液体，一瓶有毒，则只需要 $\log_2{N}$ 次检测，即可确定有毒液体。或者说，如果有 $k$ 次检测机会，那么最多可以确定 $2^k$ 瓶液体中混入的那瓶有毒液体。

这种方式，有点类似于“折半查找”，每检测一次，可以排除一半的数据集，把问题规模缩小一半。但注意，这绝对不是二分查找，或者折半查找。其实用计算机体系里的观点来看，这种问题被称为二进制问题。我们考察下上面，当 N=8 时的情况，把这 8 瓶液体按二进制编号。从 000 到 111，为了方便叙述，也把各瓶标上号，如下图。 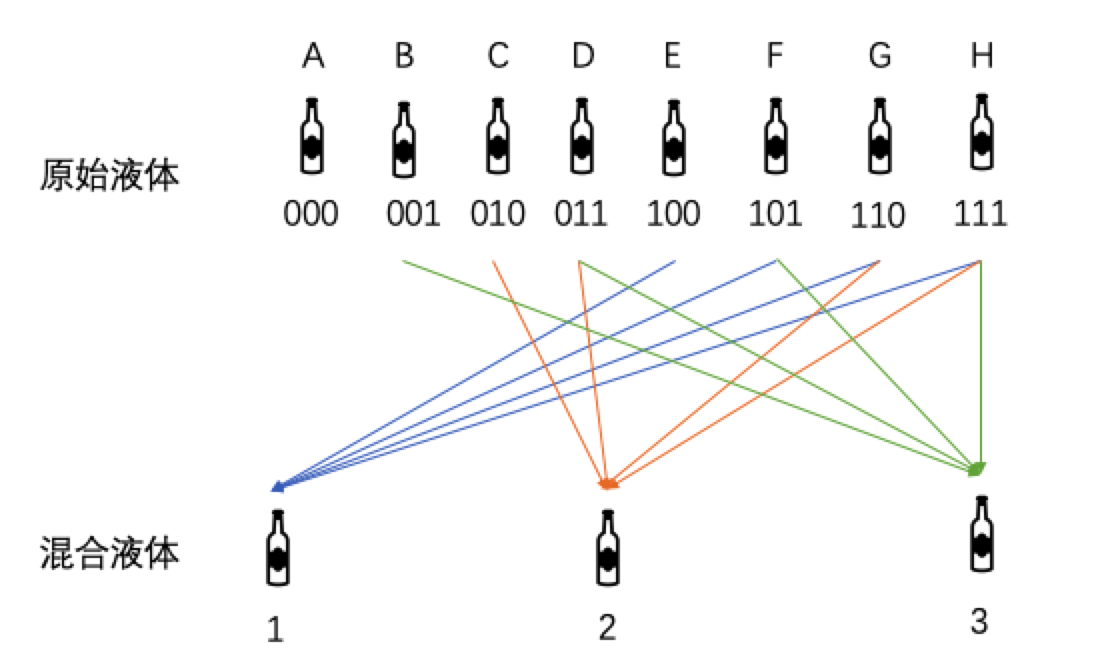然后，按每一个二进制位是否是 1 来采样混合液体，例如，E、F、G、H 可以取少量组成混合液体，因为他们的第 3 位二进制位是 1，同理 B、D、F、H 可以取少量组成混合液体，C、D、G、H 可以取少量组成混合液体。这样，我们有了 3 瓶混合液体，编号为 1、2、3，用试剂分别检测这 3 瓶混合液体，就可以确定有毒的那瓶液体的二进制编号。比如，如果 1 号变蓝，说明有毒液体肯定在 E、F、G、H 中的一个，即有毒液体那瓶的第 3 位二进制位为 1，如果 2 号变蓝，则说明有毒液体肯定在 C、D、G、H 中的一个，即有毒液体那瓶的第 2 位二进制位为 1，如果 3 号瓶没变蓝，则说明有毒液体不在 B、D、F、H 中，即有毒液体那瓶的第 1 位二进制位为 0。于是，有毒液体的那瓶二进制编号是 110，即 G 是有毒的。于是，我们检测了 3 次，最终确定了要找的那瓶有毒液体。

那么，如果有 100 瓶，则需要 7 位二进制编码，检测 7 次，即可知道有毒液体的那瓶二进制编码。

这种方法科学而高效，考察的是对二进制的理解和使用，在面试中也经常出现，这里总结了下一般思路。可能有同学已经知道用二进制方法，但真到面试时，却不知道怎么运用，给别人讲明白。还有的同学陷入一个思维误区，一上来，看到是查找问题，想当然的就套用二分查找，这也是很多人会犯的错误。