数学上的一些经典片段
最近看的几本书里,都有提到一些数学方面的知识,有些符号和公式,放在现在,可能觉得没什么,一个小学生都能看懂,但却鲜有人知道,普及这些理论,需要几代人的不懈努力和探索。有些公式和推导,都堪称数学史上的经典,这里摘取一些片段,体会下数学的美妙,也让我们看看人类的智慧是无穷的
质数是有限个吗?
质数是一个很古老的的概念,是数论中一个很重要的研究对象,大家在小学都学过。所谓质数,就是不能用两个或两个以上较小整数的乘积来表示的数,如2,3,5,7,11,13,17,等等。而 12 可以写成 2×2×3,所以就不是质数,我们称 12 这样的数为合数。显而易见,一个自然数,要么是质数,要么是合数。
关于质数,最初产生的一个问题就是:质数的个数是否是无限的呢?还是说存在一个最大的质数,即凡是比这个最大质数还大的数都可以表为几个质数的乘积呢?这个问题最初是由欧几里得提出的,同时他也给出了此问题的回答。现在我们知道,问题的答案是:有无穷多个质数。
欧几里得关于质数有无限多个的证明,至今仍然是数学推理的一个典范。他用的方法,就是现在所熟知的反证法。我们从一个尝试下的假设出发,即认为质数是有限多个,比如有 $n$ 个。即,其他任何一个数都是合数,且在 $p_1$, $p_2$ 中至少有一个能整除它。现在构造一个数 $A$ $$A={p_1} \ast {p_2} \ast \cdots \ast {p_n} + 1$$ 现在这个 $A$ ,比任何一个质数都大,因而是合数,但是我们用 $p_1$ , $p_2$ 等去除 $A$ 总是又余 1,因此这些 $p$ 不是 $A$ 的因子。这是由我们当初的假设(仅有有限个质数)而导致的矛盾,因而这个假设是不成立的,从而它的反面必然是正确的,即质数有无限多个。
以上证明说明,想找一个最大的质数是不现实的。**事实表明,即使找一个很大的质数,也是相当困难,现在计算机领域中广泛使用的非对称加密RSA的数学原理,就是基于这个事实。**迄今为止,我们找到的最大的质数是 $2^{74207281}-1$,这个数字已经很大了,长达 2233 万位!
以上即是反证法的一个经典案例,至今该方法仍然是数学家们手中论证命题的一个强有力武器。
质数的分布
质数这么多,有没有一个产生质数的通用公式呢?遗憾的是,人们做了很多次尝试,但都失败了。并没有一个公式可以做到这一点。那么,质数的分布有什么规律呢?我们用 $A_n$ 表示自然数 $1,2,3,…,n$ 中的质数个数,比如 8 以内的质数为 2,3,5,7,因此$A_8=4$, 我们查出,在 1 000 之内有 168 个质数,在 1 000 000 之内有 78 498 个,在 1 000 000 000 之内有 50 847 478 个。 我们令比值 ${A_n \over n}$ 表示前 $n$ 个自然数中质数的 “密度”,可以得出如下表:
| 数值范围 1~n | 质数个数 | 质数密度 | 1/${\ln{n}}$ | 偏差(%) |
|---|---|---|---|---|
| 1 ~ 100 | 26 | 0.260 | 0.217 | 20 |
| 1 ~ 1000 | 168 | 0.168 | 0.145 | 16 |
| 1 ~ ${10^6}$ | 78498 | 0.078498 | 0.072382 | 8 |
| 1 ~ ${10^9}$ | 50847478 | 0.050847478 | 0.048254942 | 5 |
在自然数中,单个质数的分布式不规则的,但如果把注意力集中到由比值${A_n \over n}$给出质数的分布时,会发现这种不规则消失了,这个比值所服从的简单规律,是整个数学中最著名也最值得称道的发现之一。该规律表述为:从 1 到任何自然数 $n$ 之间,所含质数的百分比,近似由 $n$ 的自然对数的倒数表示,写成数学语言,可以有以下描述: 当 $n$ 足够大时,${A_n \over n} \sim {1 \over \ln{n}}$ 白话一点,就是当 $n$ 增加时,$A_n/n \over 1/{\ln{n}}$ 趋近与 1。
质数分布的平均状态,可以用对数来描述,这是一个很引人注目的发现,两个似乎完全无关的数学概念,在事实上竟有如此紧密的联系!不得不说很令人奇怪。
这个发现,最初是由伟大的数学家高斯发现的,他当时也只是猜想,而要给出证明,他那个时代的数学是远远不够的,这个定理虽然只涉及最基本的概念,但其证明,必须用到近代数学中最有力的方法。从高斯猜想后的 100 多年,到 19 世纪末,该定理才得以完整证明。由于证明太繁琐,这里就不介绍了。
勾股定理和无理数
勾股定理,是数学中一个老少皆知的定理,在西方也叫毕达哥拉斯定理,这是一个很古老的定理,说的是在一个直角三角形中,两条直角边的平方之和,与斜边的平方相等。根据这一定理,毕达哥拉斯的一个弟子——希帕索斯,在求正方形的对角线长度时,却发现无法用一个数,或者说无法用一个等价的分数来表示它。而按照毕达哥拉斯的理论来说,世间万物的关系都可以用整数或者正数之比来表达。现在却发现,无法找到一个可以表达正方形对角线长度的数。同时,希帕索斯还用上面提到的反证法,证明了边长为 1 的正方形对角线无法用两个整数之比表示,这里给出用现代算数的一个证明。
选定正方形的边长为1,而对角线的长为$x$,根据勾股定理,有$$x^2=1^2+1^2=2$$如果现在假设可以找到两个整数 $p$ 和 $q$,使 $x={p \over q}$,则 $$p^2=2q^2$$我们假设 ${p \over q}$ 已经是不可约的,因为分子和分母的任意公因子在一开始就可约去。由于2是上式等号右边的一个因子,所以左边的 $p^2$ 是偶数,故 $p$ 本身是偶数,因为奇数的平方只能是奇数,于是我们可以写出 $p=2r$,其中 $r$ 为整数。这时上式变为 $$4r^2=2q^2,或 2r^2=q^2$$由于 2 是左边的因子,则 $q$ 必须为偶数,这样一来 $p$ 和 $q$ 同时可以被 2 整除,和 $p$, $q$ 没有公因子的假设矛盾,因此 $p^2=2q^2$ 不成立,且 $x$ 不能是有理数。
无理数的发现,是数学史上最惊人的发现之一,现在任何一个中学生都会用根号表示无理数,这个看似很普通的记法,直到近代 16 世纪才被引入!
另外一个关于无理数的有趣的结论:无理数比有理数多得多,在数轴上随便选一个点,几乎不可能选到有理数!
神秘的圆周率
第一次看到圆周率这个名词,还是读小学三年级时,教室外面的墙上,挂着各种名人照片,其中就有祖冲之,有这么一段话,大致内容就是他把圆周率精确到了小数点后面第7位,当时还不太懂什么是圆周率。这里不说 π 是什么,我们从另外一个问题,来看看这个神奇的 π。
18 世纪,数学领域开始出现一个新的分支,概率。有个法国科学家,提了一个概率问题,为了实验这个概率问题,需要有一面美国国旗,即红白条相 间的旗子。如果没有这种旗子,在一大张纸上画上若干道等距的 平行线也可以。再要一盒火柴——什么火柴都成,只要短于平行线间的距离就可以。现在把旗子铺在桌子上,扔出一根火柴,让它落在旗子上,如下图 1。它可能完全落在一条带子里,也可能压在两条带子上。 这两种情况发生的机会各为多大呢?
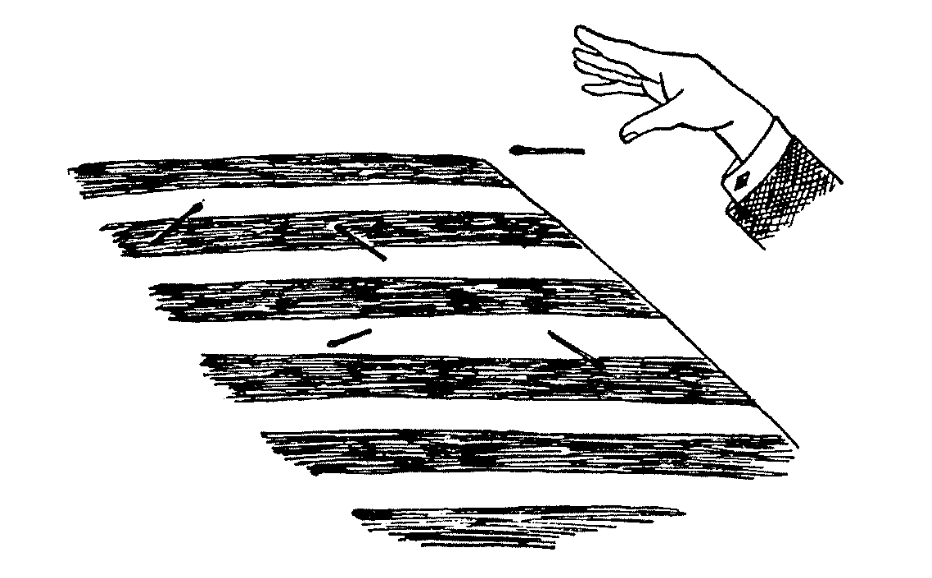 初一看,这是求概率问题,因此无非就是讨论下两种情况下的可能性,然后给个比值就行了。直觉上看,一般的概率应该都是一个确定的数,或者说有理数。然而事实真的是这样吗?
初一看,这是求概率问题,因此无非就是讨论下两种情况下的可能性,然后给个比值就行了。直觉上看,一般的概率应该都是一个确定的数,或者说有理数。然而事实真的是这样吗?
仔细考虑一下,火柴落在条带上的情况, 可由火柴中心点到最近条带边界的距离以及火柴与条带走向所成 的角度来决定,如图 2。图中给出了三种基本类型。为了简便起见,把火柴长度与条带宽度取相同数值,就说都为 2 英寸吧。如果火柴中点离边界很近,角度又较大(如例 a),火柴便与边界相交。 如果情况相反,或者角度小(如例 b),或者距离大(如例 c),火柴就全部落在一条带子里。说精确些,如果火柴的一半长度在竖直方向的投影大于从火柴中点到最近边界的距离,则火柴与边界相交(如 a),反之则不相交(如 b 和 c)。这句话可用图 2 下半部的图形表示出来。横轴以弧度为单位表示火柴落下的角度,纵轴是火柴的半长在竖直方向上的投影长度,在三角学中,这个长度叫做给定角度的正弦。显然,当角度为零时,正弦值也为零,因为这时火柴呈水平方向。当角度为 ${π \over 2}$ 即直角时,火柴取直立位置,与其投影重合,正弦值就是 1。对于处于两者之间的角度,其正弦的值由大家所熟悉的正弦曲线给出。
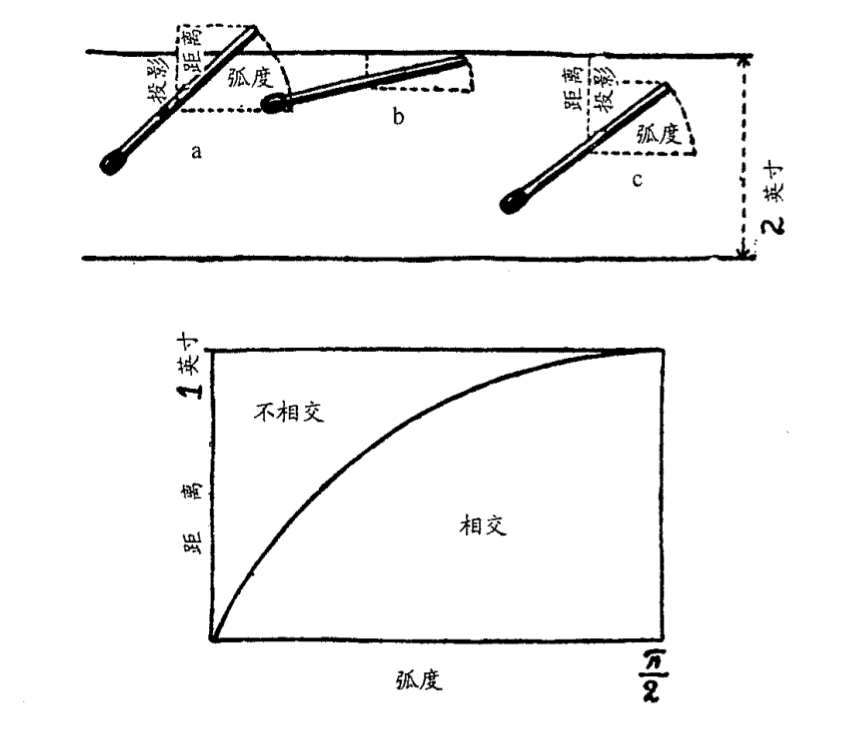
有了这条曲线,要计算火柴与边界相交或不相交的两种机会 就很方便了。事实上,我们已经看到(再看图 2 上部的三个例 子 ), 火柴中点离边界的距离如果小于半根火柴的竖直投影,即小于此时的正弦值,火柴就会与边界相交。这时,代表这个距离和角 度的点在正弦曲线之下。与此相反,火柴完全落在一个条带内时, 相应的点在曲线之上。
按照计算概率的规则,相交机会与不相交机会的比值等于曲 线下的面积与曲线上的面积的比值。也就是说,两个事件的概率, 各等于自己的那一块面积除以整个矩形的面积。可以由数学上证明,图中正弦曲线下的面积恰好等于 1。而整个矩形的面积为 ${\pi \over 2}$$\times 1$= ${\pi \over 2}$。我们得出结论:**火柴与边界相交的概率为 ${1 \over {π/2}}={2 \over π}$ **
最后,一个勤劳的意大利数学家,做了这件无聊的事,他扔掷了 3407 根火柴,数一数有 2169 根与边界相交。以这个真实数据代入布丰公式,π 就变成了 ${2 * 3407 \over 2169}$,即 3.1415929,与精确值比,一直到第七位才开始不同!
这个例子对概率定律的实用性无疑是一个极有趣的明证。一个概率实验,居然能和 π 撤上关系!一方面证明了概率理论是正确的,因为由概率推出的数据和事实相符,另一方面,如果我们的祖先知道还能这么玩,根本不用掌握什么高深的技巧,直接扔针或者扔火柴,扔个十天半月的,只要扔的次数足够多,即可精确的估算出 π 的大小!
小结
本文仅仅摘取了几个很小的关于数学的片段,让大家体会下数学的魅力和美妙。也许有些理论或定理,我们在小学都学过,有的证明,我们也都能一看就懂,这里面都包含着严密的逻辑和推理过程,任何一条公式,理论,绝不是某个人上帝附体,或者灵光一闪而提出的,都是一个不断探索和积累的过程。人类的这种推理和思考过程,使我们和一般的动物有着本质的区别。这种能动性,让我们了解世界,进而改变世界。
参考
- 《什么是数学》
- 《从一到无穷大》
- 原文作者:JimmyXu
- 原文链接:http://xujimmy.com/2018/03/22/about-mathematical-formula.html
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。